Bezier-ish by points & Way better Bezier-ish by Points
Spline Type 3
Revit/Vasari has a couple kinds of splines, regular spline (A) and spline-by-points (B). You’d think they were pretty similar, but you’d be wrong. I’d like to show an alternative to these 2 curve types, (C), a point hosted control polygon based curve.
Regular Spline, sometimes called a b-spline, has a control polygon and a weighted “attraction” to the placement points while Spline-by-points passes precisely through it’s placement points. Perhaps more important, the Spline-by-points is much easier to associate with other geometry, flexing and stretching with it’s host in a way that is not possible with the regular spline tool, and it is also a 3 dimensional curve that is not restricted to one plane.
So what can you do if you want the weighted polygon behavior but want to keep the associations between the curve and a host?
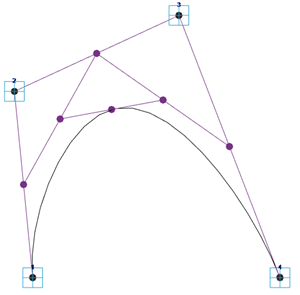
As previously discussed, Revit/Vasari has a couple kinds of splines (regular spline and spline-by-points) that you’d think they were pretty similar (but you’d be wrong). I made some tools to improve on this situation using Adaptive Components, but have refined this method. This image shows 3, 4, and 5 point spline-by-point curves inside of an adaptive component rig, superimposed on a regular control polygon spline to illustrate the divergence (There’s not much difference, but double click to take a closer look).
It uses the same methods as shown in this post but does further subdivisions of the control polygons for greater accuracy and flexibility.
A couple of things I noticed. Most significant, the tangency conditions at the start and end are very close approximations. 99 times out of 100, this should be fine. Here is an example of when it falls down:
On the left, two real b-splines drawn coming to tangency conditions. On the right, the 4 point adaptive component spline by point family.
Because the curves come together into a near tangent, but not quite, they slightly overlap. It isn’t visible even zoomed WAY in.
But the result is that you can’t create a form element from the fake b-splines, because it will create a self intersecting form, but the real b-splines can.
[Clarification: This failure is kind of hard to reproduce, it doesn’t happen for all situations even like the one shown, there is a similar geometry in the sample files, and it works perfectly. I think it has to be of a particular really huge scale. In general, you can use this to make forms just fine, as shown inthis post. Here is an exaggerated view of what is happening the joint between the 2 curves at a bazillion times magnification:
Again, I have a hard time reproducing this problem, but it can be done. If you’re worried about it, experiment a little. ]
The other issue that is a bit more obscure, is the four point 4 spline doesn’t create a proper cusp when you do a crossed rectangle (shown here, a rectangle with points going 1, 3,2,4 in clockwise order) as a real bezier does. Rather, it makes a bump.
Spline Type 3
Revit/Vasari has a couple kinds of splines, regular spline (A) and spline-by-points (B). You’d think they were pretty similar, but you’d be wrong. I’d like to show an alternative to these 2 curve types, (C), a point hosted control polygon based curve.
Regular Spline, sometimes called a b-spline, has a control polygon and a weighted “attraction” to the placement points while Spline-by-points passes precisely through it’s placement points. Perhaps more important, the Spline-by-points is much easier to associate with other geometry, flexing and stretching with it’s host in a way that is not possible with the regular spline tool, and it is also a 3 dimensional curve that is not restricted to one plane.
So what can you do if you want the weighted polygon behavior but want to keep the associations between the curve and a host?
As previously discussed, Revit/Vasari has a couple kinds of splines (regular spline and spline-by-points) that you’d think they were pretty similar (but you’d be wrong). I made some tools to improve on this situation using Adaptive Components, but have refined this method. This image shows 3, 4, and 5 point spline-by-point curves inside of an adaptive component rig, superimposed on a regular control polygon spline to illustrate the divergence (There’s not much difference, but double click to take a closer look).
It uses the same methods as shown in this post but does further subdivisions of the control polygons for greater accuracy and flexibility.
A couple of things I noticed. Most significant, the tangency conditions at the start and end are very close approximations. 99 times out of 100, this should be fine. Here is an example of when it falls down:
On the left, two real b-splines drawn coming to tangency conditions. On the right, the 4 point adaptive component spline by point family.
Because the curves come together into a near tangent, but not quite, they slightly overlap. It isn’t visible even zoomed WAY in.
But the result is that you can’t create a form element from the fake b-splines, because it will create a self intersecting form, but the real b-splines can.
[Clarification: This failure is kind of hard to reproduce, it doesn’t happen for all situations even like the one shown, there is a similar geometry in the sample files, and it works perfectly. I think it has to be of a particular really huge scale. In general, you can use this to make forms just fine, as shown inthis post. Here is an exaggerated view of what is happening the joint between the 2 curves at a bazillion times magnification:
Again, I have a hard time reproducing this problem, but it can be done. If you’re worried about it, experiment a little. ]
The other issue that is a bit more obscure, is the four point 4 spline doesn’t create a proper cusp when you do a crossed rectangle (shown here, a rectangle with points going 1, 3,2,4 in clockwise order) as a real bezier does. Rather, it makes a bump.